
要做好深度学习任务不妨先在损失函数上做好文章
雷锋网 AI 科技评论按:损失函数对于机器学习而言,是最基础也最重要的环节之一,因此在损失函数上「做好文章」,是一个机器学习项目顺利进行的前提之一。Deep Learning Demystified 编辑、数据科学家 Harsha Bommana 以浅显易懂的文字介绍了在不同的深度学习任务中如何设置损失函数,以期大家能够对损失函数有一个更加清晰的认识。雷锋网 AI 科技评论编译如下。
在所有的机器学习项目中,损失函数的设置是确保模型以预期的方式工作的最重要的步骤之一。损失函数能够给神经网络的实际应用带来很大的灵活性,并且能够明确该神经网络的输出究竟如何与其他的网络连接。
从预测连续值如月度支出到划分离散类如对猫和狗进行分类等,都是神经网络能够执行的任务。各不相同的任务需要不同类别的损失,因为这些任务的输出格式各不相同。对于非常特定的任务而言,我们需要明确希望如何定义这一损失。
简单而言,损失函数(J)可以被定义为包含两个参数的函数:
- 1. 预测的输出
- 2. 实际的输出

神经网络损失可视化
该函数通过比较模型预测的值与其应该输出的实际值来计算出模型表现的糟糕程度。如果 Y_pred 与 Y 相差很大,损失值就会很高;如果两个值几乎一样,损失值就会很低。因此,我们需要让损失函数在数据集上训练时,始终能够有效地对模型进行惩罚。
如果损失非常大,损失值在模型训练期间会传递到整个网络中,同时,权重的变化会比平时要大很多。如果损失较小,权重的变化就不会这么大了,因为网络已经能够很好地执行任务了。
这一情况某种程度上跟考生准备考试差不多,如果考生考出的成绩很糟,我们就可以说损失非常大,那这位考生就需要对自己为下次考试所做的准备工作进行大改,以便在下次考试中取得更好的成绩。然而,如果考生的考试成绩还不错的话,他们就不会过多调整已经为下次考试所做的准备工作。
现在,让我们以分类任务为例,来了解损失函数在该示例中到底是如何表现的。
分类损失
当神经网络试图预测一个离散值时,我们可以将其视作一个分类模型。该网络会预测出图像呈现的是什么动物类别,或邮件是否是垃圾邮件。首先,让我们看下分类任务中神经网络如何表示输出。

分类神经网络输出格式
输出层的节点数量取决于用数据表示的类的数量。每一个节点都代表一个单类。每个输出节点的值基本上都表示模型将类分类正确的概率。
Pr(Class 1) = Probability of Class 1 being the correct class
一旦我们得到了所有不同类的概率,我们将概率最高的类视为该示例中预测的类。让我们从探索二元分类如何实现开始。
二元分类(Binary Classification)
在二元分类中,即便我们在两个类之间进行预测,输出层中也仅有唯一的一个节点。为了得到概率格式的输出,我们需要应用一个激活函数。由于概率值在 0 和 1 之间,我们使用能够将任意实际值压缩为 0 到 1 之间的值的 Sigmoid 函数。
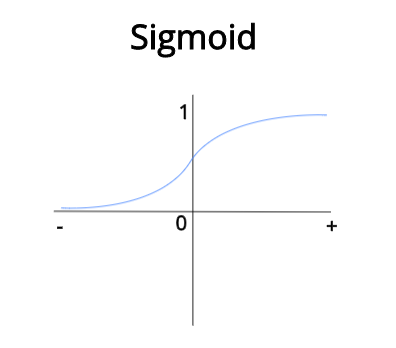
Sigmoid 函数图可视化
当 Sigmoid 函数中的输入变大并趋向于正无穷时,该函数的输出值会趋近于 1。与此同时,当输入趋向于负无穷时,该函数的输出值会趋近于 0。现在我们就总能够得到一个在 0 到 1 之间的值,而这恰恰就是我们所需要的取值范围,因为我们要用到概率。
如果输出值大于 0.5(50% 的概率),我们将类视为从属于正类 (Positive class);如果输出值低于 0.5,则将类视为从属于负类(negative class)。例如,假如我们训练一个网络来对猫和狗进行分类,我们可以将狗分为正类,这样的话,狗在数据集中的输出值就是 1;同样地,我们将猫分为负类,猫的输出值就是 0。
我们为二元分类使用的损失函数叫做二元交叉熵(Binary Cross Entropy,BCE)。该函数能够对二元分类任务的神经网络进行有效地惩罚。下图为该函数的表现形式:

二元交叉熵损失图
我们可以看到,它有两个分离的函数,它们各自表示 Y 的取值。当我们需要预测正类(Y=1)时,我们使用:
Loss = -log(Y_pred)
当我们需要预测负类(Y-=0)时,我们使用:
Loss = -log(1-Y_pred)
如图所示,在第一个函数中,当 Y_pred 等于 1 时,损失值就等于 0,这就能够起到作用,因为 Y_pred 恰好与 Y 相等。当 Y_pred 的值趋近于 0 时,我们可以看到损失值会一路增加到一个非常高的概率,并且当 Y_pred 变成 0 时,损失值会变成无穷大。这是因为从分类的角度而言,0 和 1 就是两个极端——因为它们各自表示完全不同的类。因此当 Y_pred 等于 0、Y 等于 1 时,损失值就变得非常高,从而让网络更加有效地学习它的错误。

二元分类损失对比
我们可以用数学的方式,将整个损失函数表示为如下方程式:
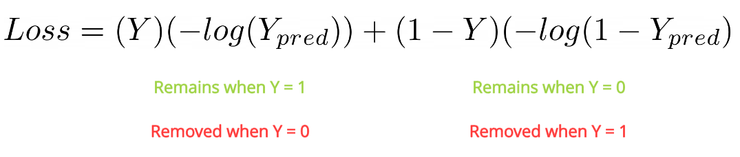
二元交叉熵方程式
该损失函数也叫做对数损失(Log Loss),以上就是该损失函数者针对二元分类神经网络任务的执行方式。接下来让我们来看看多类分类网络中如何定义损失。
多类分类(Multiclass Classification)
当我们每次都需要让模型预测出一个可能的类别时,多类分类是比较合适的方式。由于我们依旧需要处理概率问题,所以对所有输出的节点使用 Sigmoid 函数会比较有用,这样的话所有的输出就都在 0 到 1 之间取值,不过,这种方法也存在一个问题:当我们考虑多个类别的概率时,我们需要确保所有单个类别的概率的总值等于 1,这也是由概率的属性所决定的。然而,使用 Sigmoid 函数并不能确保总值都等于 1,因此我们需要用到另外的激活函数。
在该示例中,我们使用的激活函数是 Softmax 函数。该函数能够确保所有的输出节点的取值都在 0 到 1 之间,并且所有输出节点的总值都等于 1。Softmax 的公式如下:

Softmax 公式
我们不妨用一个示例将 Softmax 可视化:

Softmax 示例可视化
如上图所示,我们可以简单将所有的取值变成一个指数函数。之后,为了确保所有取值都在 0 到 1 的范围内以及所有输出值的总值等于 1,我们还需要用所有指数的总和来除以单个指数。
所以为什么我们在将每个值正则化之前,要先将每个值指数化?为什么不能仅仅正则化值本身?这是因为,Softmax 函数的目标是确保一个输出值足够大(趋近于 1)而另外所有的输出值足够小(趋近于 0)。Softmax 函数采用指数的方式,就是为了确保能够做到这一点。而之后我们对值进行正则化处理则是因为我们需要用到概率。
既然现在输出都能够以合适的格式表示出来了,下面我们来看看如何针对该格式设置损失函数。好的一面是,这里用到的损失函数基本上与二元分类中用到的损失函数差不多。我们仅仅需要根据每个输出节点对应的目标值在每个输出节点上使用损失函数,然后我们就能够得到所有输出节点的对数损失总值。

多分类交叉熵可视化
该损失就叫做多分类交叉熵(Categorical Cross Entropy)。后续我们再来看看分类任务中的一个特例——多标签分类。
多标签分类(Multilabel Classification)
当你的模型需要预测多类别作为输出时,就要用到多标签法分类。例如,假设你在训练一个神经网络来预测一张食物图片上显示的食材,这时,网络就需要预测多种食材,因而 Y 中就可能出现多个取值为 1 的输出。
对此,我们仅靠使用 Softmax 函数是无法完成该分类任务的,因为 Softmax 函数往往只能让一个类别输出为 1,而其他的所有类别都输出为 0。所以,在这个任务上,我们仅仅继续对所有输出节点值使用 Softmax 函数,因为我们依旧还需要预测出每个类别的单个概率。
而针对该分类任务的损失,我们可以直接对每个输出节点使用对数损失函数并取总值,这跟我们在多类分类任务中的工作一样。
做好分类以后,我们下面要做的是回归。
回归损失
在回归中,我们的模型尝试预测一个连续值。一些回归模型的示例有:
- 房价预测
- 人的年龄预测
- ……
在回归模型中,神经网络会针对模型需要预测的每个连续值输出一个节点,之后直接通过比较输出值和实际值来计算回归损失。
回归模型中最常用的损失函数是均方误差(Mean-Square Erro)损失函数。我们通过使用该函数,仅需要计算出 Y_pred 和 Y 的方差,然后再将所有取值得到的方差平均即可。我们假设有 n 个取值点:

均方误差损失函数
这里的 Y_i 和 Y_pred_i 指的是数据集中的第 i 个 Y 值和神经网络对同一个取值所得出的对应的 Y_pred。
以上是本文的全部内容。希望各位读者通过阅读此文,能够对深度学习的不同任务如何设置损失函数有一个更加清晰的认识。
via https://medium.com/deep-learning-demystified/loss-functions-explained-3098e8ff2b27





